从某种意义上，范数相当于对实数绝对值得 一种推广，以解决衡量求解线性方程组近似解的准确程度和研究迭代法收敛性问题。本文主要介绍向量范数与矩阵范数，利用这些范数进行误差分析和评判线性方程组的性态。

向量范数

首先明确向量范数是非负实数，且设$f(x)=||x||$是定义在$\mathrm{R}^n$上的非负实质函数，若$||x||$满足以下三条：

• $|x| \geqslant 0, \quad|x|=0 \Leftrightarrow x=0$;
• $\forall \alpha \in \mathbf{R},\|\alpha A\|=|\alpha|\|A\|$;
• $\|x+y\| \leqslant\|x\|+\|y\|$ (三角不等式),

则称$\|x\|$为$\mathrm {R}^n$上的向量范数，由三角不等式可以推得
$$
||x|-|y|| \leq |x-y|
$$
其实考试也就会问问常见向量范数的计算：
$$
\|x\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right|(向量的 1 范数);
$$
$$
\|x\|_{2}=\left(\sum_{i=1}^{n} x_{i}^{2}\right)^{\frac{1}{2}} (向量的 2 范数);
$$
$$
\|x\|_{\infty}=\max _{1 \leqslant i \leqslant n}\left|x_{i}\right|(向量的 \infty 范数).
$$
利用向量范数定义 $x$ 的近似向量 $\tilde{x}$ 的绝对误差与相对误差如下:
绝对误差: $\|\Delta x\|=\|x-\tilde{x}\|$;
相对误差: $\frac{\|\Delta x\|}{\|x\|}=\frac{\|x-\tilde{x}\|}{\|x\|}$.

矩阵范数

矩阵范数的定义

首先明确矩阵范数也是是非负实数，且设$f(A)=||A||$是定义在$\mathrm{R}^{n \times n}$上的非负实质函数，若$||A||$满足以下四条：

(1) $\|A\| \geqslant 0,\|A\|=0 \Leftrightarrow A=O$;
(2) $\forall \alpha \in \mathbf{R},\|\alpha A\|=|\alpha|\|A\|$;
(3) $\|A+B\| \leqslant\|A\|+\|B\|$ (三角不等式);
(4) $\|A B\| \leqslant\|A\|\|B\|$,

则称$|A|$为$\mathrm{R}^{n \times n}$上的矩阵范数。

矩阵的算子范数

矩阵的算子范数: 设 $x \in \mathbf{R}^{n}, A \in \mathbf{R}^{n \times n},\|x\|_{p}(p=1,2, \infty)$ 是给定的一种向量范数, 相应地定义一个矩阵的非负函数
$$
\|A\|_{p}=\max _{x \neq 0} \frac{\|A x\|_{p}}{\|x\|_{p}}=\max _{\|x\|_{p}=1}\|A x\|_{p}
$$

则 $\|A\|_{p}$ 是一种矩阵范数, 称为矩阵 $A$ 的算子范数, 并且满足相容性条件
$$
\|Ax\|_p \leq \|A\|_p\|x\|_p
$$
设 $x \in \mathbf{R}^{n}, A \in \mathbf{R}^{n \times n}$, 按式定义可得确定的对应于向量的三种范 数 $\|x\|_{p}(p=1,2, \infty)$ 的矩阵范数分别为
(1) $\|A\|_{1}=\max\limits _{1 \leqslant j \leqslant n}\left\{\sum_{i=1}^{n}\left|a_{i j}\right|\right\} \quad(1$ 范数或列范数);
(2) $\|A\|_{2}=\sqrt{\lambda_{\max }\left(A^{\mathrm{T}} A\right)}$ (2 范数或谱范数);
(3) $\|A\|_{\infty}=\max\limits _{1 \leqslant i \leqslant n}\left\{\sum_{j=1}^{n}\left|a_{i j}\right|\right\} \quad(\infty$ 范数或行范数), 其中 $\lambda_{\max }\left(A^{\mathrm{T}} A\right)$ 表示矩阵 $A^{\mathrm{T}} A$ 最大的特征值.

条件数

定义 设 $A$ 是非奇异矩阵, 数
$$
\operatorname{Cond}(A) \triangleq\|A\|\left\|A^{-1}\right\|
$$
称为矩阵 $A$ 的条件数. 条件数与矩阵的范数有关, 也将条件数记为
$$
\operatorname{Cond}_{p}(A) \triangleq\|A\|_{p}\left\|A^{-1}\right\|_{p}, \quad p=1,2, \infty .
$$
常用的矩阵条件数为
(1) $\operatorname{Cond}_{\infty}(A)=\|A\|_{\infty}\left\|A^{-}\right\|_{\infty}$;
(2) $\operatorname{Cond}_{2}(A)=\|A\|_{2}\left\|A^{-1}\right\|_{2}=\sqrt{\frac{\lambda_{\max }\left(A^{\mathrm{T}} A\right)}{\lambda_{\min }\left(A^{\mathrm{T}} A\right)}}$.

当$A$为对称矩阵时，$\operatorname{Cond}_{2}(A)=\frac{|\lambda_1|}{|\lambda_n|}$, 其中$\lambda_1$，$\lambda_n$分别为矩阵$A$的绝对值最大和绝对值最小的特征值。

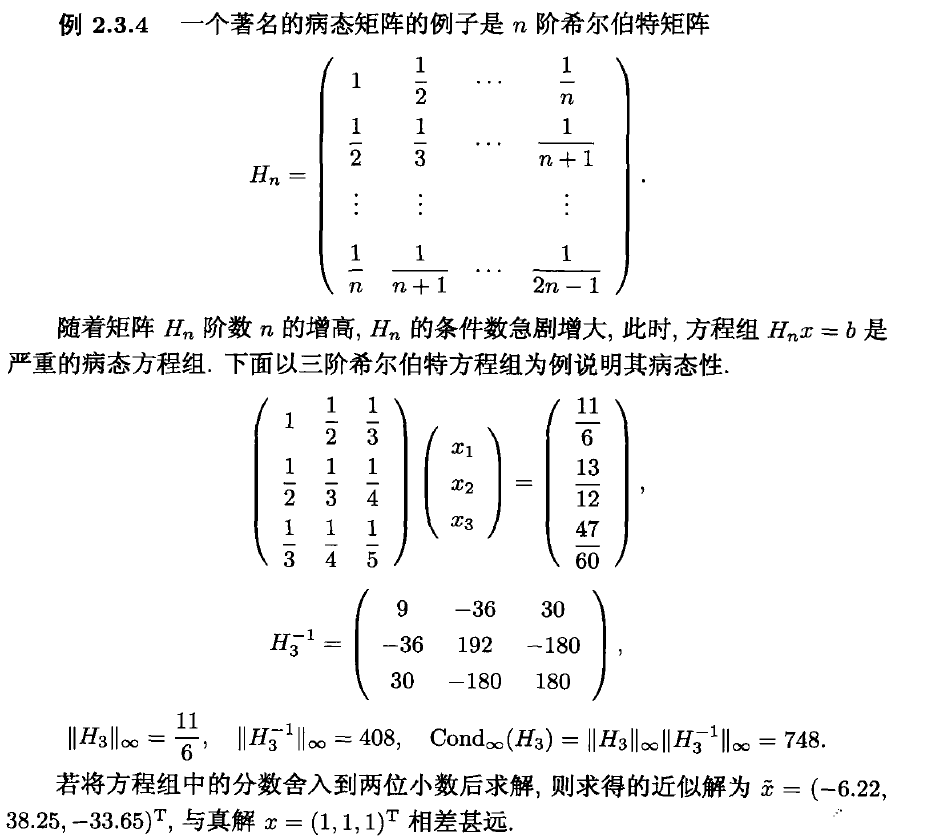
矩阵的条件数刻画了方程组的性态，条件数大的矩阵称为“病态”矩阵，相应的方程组称之为“病态方程组”；条件数小的矩阵称为“良性”矩阵，相应的方程组称为“良态”方程组,下面给出病态矩阵的例子